Principle：
- Acquisition stage: Perform special sampling on the video in the time domain (not traditional uniform and complete sampling). Data that is much less than the complete data volume of the original video is collected through specific sampling strategies and patterns.
- Processing stage: Utilize the characteristics such as correlation and sparsity of the video in the time domain as well as mathematical algorithms and other means to process and analyze the small amount of collected data.
- Recovery stage: Through complex reconstruction algorithms and operations and other processes, the original video or its approximate video (within a certain accuracy range) is recovered from these small amounts of data.
Compressive sensing is also known as compressed sampling, sparse sampling, and compressive sensing. If a signal is sparse or compressible after a certain transformation (such as wavelet transform, Fourier transform, etc.), a measurement matrix independent of the transformation basis can be designed to measure the original signal. The obtained measurement signal can achieve accurate or approximate reconstruction of the signal by solving a nonlinear optimization problem. The dimension of the measurement signal is much smaller than that of the original signal, and the measurement signal only contains important information of the signal. The theoretical framework of compressive sensing is shown in the figure below.
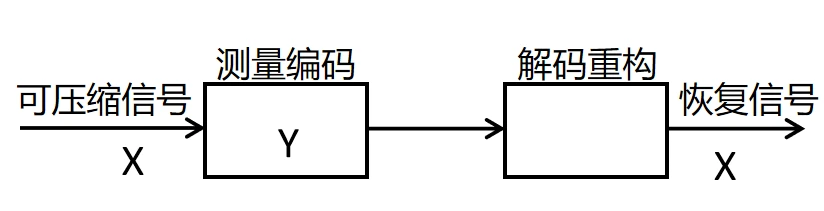
The compressive sensing theory combines compression and sampling and performs non-adaptive measurement coding on signals at a rate much lower than the Nyquist sampling rate. It breaks through the bottleneck of Shannon's sampling theorem and makes the acquisition of high-resolution signals possible. The application of compressive sensing greatly reduces the measurement time, sampling rate, and the number of measurement devices. In compressive sensing, after a signal undergoes sparse transformation, the transformed domain signal can be regarded as a concise expression of the original signal. The ability of a signal to be sparsely represented is a prior condition of the compressive sensing theory. Mathematical definition of sparsity: The transform coefficient vector of signal X under the orthogonal basis 
is 
，
Suppose for 
and 
，the coefficient vector satisfies:
This indicates that the coefficient vector is sparse in a certain sense. If the cardinality of the support domain 
of the transform coefficient 
is not greater than K, then the signal X is said to be sparse and has a sparsity of K.
The foundation and prerequisite for the application of compressive sensing theory is to find the optimal sparse domain of the signal. Only by representing the signal under an appropriate sparse basis can the sparsity of the signal be guaranteed and the sparsity of the signal be made as small as possible. This not only can ensure the recovery accuracy of the signal but also can improve the signal acquisition speed, which is conducive to reducing the resources required for storing and transmitting the signal. When studying the sparse representation of a signal, the sparse representation ability of the sparse basis can be measured by the decay rate of the sorted transform coefficients. If the transform coefficients satisfy power decay and gradually approach zero after being sorted, then the signal is called a compressible signal. This signal can be encoded and reconstructed by using compressive sensing technology, and the reconstruction error satisfies:
Where 
and 
are constants. Signals of smooth signals after Fourier transform and wavelet transform, as well as image signals with discontinuous edges after Curvelet transform all have sufficient sparsity. Therefore, compressive sensing technology can be used for measurement and reconstruction.
Encoding process of CS frames:
First, divide the CS frames into equally sized non-overlapping image blocks. Scan each image block into a one-dimensional signal through certain rules (such as by row, by column, or by ZigZag). Then, perform block-based measurement on the CS frames using a random measurement matrix. Finally, transfer the measured values directly to the decoding end in sequence, or transfer the quantized measured values to the decoding end in sequence.
Decoding process of CS frames:
If the signal transmitted from the encoding end is a quantized signal, then at the decoding end, correspondingly, first perform inverse quantization on the received signal and then reconstruct it. Otherwise, directly enter the reconstruction step. In order to improve the quality of the reconstructed video frames, use the reconstructed key frames or the neighborhood image blocks of the corresponding macroblocks of adjacent reconstructed video frames to construct a dictionary. Use this dictionary instead of a fixed sparse basis such as a discrete cosine transform matrix. Due to temporal correlation, video signals have stronger sparsity. Therefore, under the condition of the same number of measured values, CS frames have higher reconstruction quality. However, due to a certain error between the reconstructed video frames and the original video frames, when constructing a dictionary for adjacent subsequent video frames for sparse reconstruction using the reconstructed CS frames within a group at the decoding end, error propagation phenomenon will occur. Use motion estimation and motion compensation technology or block prediction technology in traditional distributed video coding to generate side information. This side information can be regarded as an estimate of the original video frames. Using side information to assist sparse reconstruction algorithms can accelerate the convergence speed of the reconstruction algorithm and the reconstruction quality of video signals.
The signal reconstruction algorithm is the core of compressive sensing theory and refers to the process of reconstructing a sparse signal or a compressible signal of length 
from M measured values.
1、Basis pursuit algorithm
This algorithm uses the conclusion that the minimum 1-norm has the same solution as the minimum 0-norm under certain conditions. Replacing the 0-norm with the 1-norm, the following formula is obtained:
Considering the presence of noise or allowing a certain reconstruction error, the above formula can be converted into:
Where，
is the reconstruction error.
The basic idea of the matching pursuit algorithm is to gradually solve the sparse solution of the signal by searching for the atom that best matches the signal from the overcomplete dictionary through an iterative method. Each iteration in this algorithm contains two steps: atom selection and signal residual update. Atom selection is to select the atom that best matches the current residual from the overcomplete dictionary. The corresponding projection length is used to measure the correlation. Signal residual update is to subtract the relevant part from the residual as the updated residual signal.
Suppose the atoms in the overcomplete dictionary are 
and 
，That is, the
column vector in the projection matrix is ，All atoms have been unit normalized. Then the atom selection algorithm in the j-th iteration is as follows:
In the formula,
represents the inner product,，
represents the residual after the
-th iteration, the initial residual signal is the original signal, 
represents the coefficient related to the best-matching atom selected in this iteration, denoted as 
. Then the algorithm updates the residual signal according to the following formula:
If the termination condition is satisfied, such as when the approximation residual is less than the expected approximation error limit, the algorithm ends.
In the matching pursuit algorithm, the projection of the signal on the selected atom set is non-orthogonal, which makes the result of each iteration possibly suboptimal. Therefore, the algorithm may require many iterations to converge, and the sparsity of the approximation result of this algorithm is poor.
The orthogonal matching pursuit algorithm effectively overcomes the shortcomings of the matching pursuit algorithm. The atom selection criterion in this algorithm is the same as that in the matching pursuit algorithm. Only in each step of the iteration, all selected atoms are orthogonalized to ensure the optimality of the iteration, thereby reducing the number of iterations, increasing the convergence speed, and improving the sparsity of the approximated signal. Experiments show that for a fixed K-sparse N-dimensional discrete-time signal x, when measured with a Gaussian matrix of
,as long as 
, the orthogonal matching pursuit algorithm can accurately reconstruct the signal with a very high probability and is faster than the basis pursuit algorithm.
The orthogonal matching pursuit algorithm assisted by prior knowledge is based on the OMP algorithm. The decoder uses prior knowledge to assist in signal reconstruction. The prior knowledge obtained by the decoder is to estimate the position of the important elements of the current signal according to the position of the important elements (non-zero large coefficients) of the already reconstructed signal. This prior knowledge for estimating the position of important elements is not necessarily completely correct and may have some errors. So when using these prior knowledge, there must be an error correction mechanism. With the assistance of these prior knowledge, the signal reconstruction process of the orthogonal matching pursuit algorithm assisted by prior knowledge is much faster than that of the normal orthogonal matching pursuit algorithm. However, the signal reconstruction recovery quality of the orthogonal matching pursuit algorithm assisted by prior knowledge is not inferior to that of the normal orthogonal matching pursuit algorithm, and the computational complexity is greatly reduced.
For the original image with different compression rates or sparsity set, the success rates of these two algorithms in perfectly or approximately perfectly reconstructing the image are very high. The matching pursuit method is usually relatively fast, while the basis pursuit algorithm is relatively accurate when considering noise.
Both the BP and OMP algorithms are reconstruction algorithms based on the sparsity or compressibility of the signal in a certain transform domain. However, the minimum total variation method (TV) abandons this idea and instead realizes signal reconstruction by minimizing a specific energy function. Moreover, this algorithm is specifically used to process two-dimensional image and video signals. The specific algorithm idea is as follows:
Where x is a two-dimensional image signal, 
is the Frobenius operator, and ε>0 is the reconstruction error. Assuming 
is a two-dimensional discrete signal, then
represents the sum of the magnitudes of the gradients of each pixel point of a two-dimensional image signal. This part is mainly contributed by noise. Therefore, the basic idea of the algorithm is to minimize the noise of the recovered signal while ensuring the reconstruction error. In addition to being used for signal reconstruction, this algorithm is particularly suitable for denoising and deblurring image and video signals. In general, the reconstruction algorithms that have appeared in compressive sensing so far can be roughly divided into the following three categories:
- Convex relaxation algorithms: To find the sparse approximation of a signal, this type of algorithm transforms non-convex optimization problems into convex optimization problems for solution, such as the basis pursuit algorithm, gradient projection method, interior point method, and iterative threshold method.
- Greedy pursuit algorithms: This type of method gradually approximates the original signal through an iterative method and solves for a sparse coefficient in each iteration. This type of algorithm mainly includes the matching pursuit algorithm, OMP algorithm, stagewise OMP (StOMP) algorithm, and regularized OMP (ROMP) algorithm.
- Combinatorial algorithms: This type of method requires that the sampling support of the signal can be quickly reconstructed through group testing, such as Fourier sampling, chain pursuit, and HHS (HeavgHitters Oil Steroids) pursuit.
The visual software operation interface integrates module drive control on the software, which is convenient to use.
Testing result：
Main hardware list
| Categories | Specification and Model | Unit | Quantity |
| DMD SLM | F4320 DDR 0.7XGA | set | 1 |
| Area array camera | 3.2 million pixels | piece | 1 |
| Telecentric lens | Magnification ratio 0.5 | piece | 1 |
| Telecentric lens | Magnification ratio 1 | piece | 1 |
| Fixed focus lens | 25mm focal length, 10 million pixels | piece | 1 |
| TIR prism | K9 | piece | 1 |
| Bracket | Including base plate, connecting rod, rod holder, fork block, threaded adapter, fine-tuning platform, base, mirror bracket, M6 screws (several) | set | 1 |
| Tool | Breadboard handle | set | 1 |
| LED light | 120W | piece | 1 |
Compared with traditional video compression techniques, it may have a higher compression ratio in specific scenarios; it can alleviate the contradiction between the temporal and spatial resolutions in traditional video processing to a certain extent; it is of great significance for some application scenarios with limited resources (such as limited storage capacity and limited transmission bandwidth).
